'Interpreted Predicate Logic' Ontologies
What they are, and where they can be used for.
Frans A. Meijs

Introduction

This document assumes that the reader has knowledge of the principles of modern computer programming. The theories it presents are written in the Interpreted Predicate Notation. They form an representational ontology[1]: a grammar and corresponding rules, intended for writing, simulating and verifying models of object worlds [Hofweber T. 2004]. Such a model is essentially a data base containing propositions (Prolog "facts") about the object world. From this viewpoint, the theories presented in this document specify the rules and constraints applicable to the contents of the data base. For verifying the specification, the Prolog facts are read by a Prolog interpreter, together with the theories. 


    specification -->
                         Prolog interpreter ---> report
    theories ------->

Fig.1: Verifying a specification

The specification together with the theories form a set of axioms about the object world. Constraints on the object world are referred to as invariants Although constants in the object world are also essentially invariant we will stick to the computer science tradition of reserving the term for this type of constraints, and are specified in IPL as contradictions, predicates about states which are unwanted or which cannot exist in the object world [Goebel R. 1986]. States about which no predicate or proposition other than a contradiction have been specified are by default false (the closed world assumption)For the author of a specification, the invariants can be seen as "design rules". These invariants together with the Prolog syntax rules make up the constraints for well-formedness of the sentences in the theories..

Once the interpreter has consulted all files without detecting syntax errors, a query has to be done for contradiction(X), to effectuate the check. As soon as the interpreter has found no contradictions, the spec can be queried for further analysis. For example, on the query entity(X) the interpreter will report all instances of the class of entities, as well as of all its subclasses.

The theories are based on proven technology as much as possible:

Organization of the document

The theories are presented in order of increasing detail (decreasing level of abstraction). Please be patient when reading this document; the meaning of the theories becomes clear only after a number of reading iterations between the abstract theories and the more detailed theories. Concepts are defined by the way they are associated. There is no better solution to formal definition; attempts to find one have failed so far [Kant I. 2007] p.xxxiii;   [Wittgenstein 1953]

Basic concepts

Let us start with an example of how everyday's communication of information can go wrong. For "information" you may read "knowledge" as well. If you ask a little child by telephone where it is, it is very likely that it will say: I'm here!. Obviously little children still have to learn that what "here" is for them, might be meaningless for somebody else.

But even adults make this kind of mistake. While talking, they make a lot of preassumptions, and they assume - without verifying - that the listener makes the same preassumptions.

As another example, suppose a person A sees a table - a piece of furniture - while a person B can not see it. When person A says to person B: That table is red, we may wonder whether person B perceives the table in exactly the same way as person A does. This needs not to be so, because:

The examples show that when one person is talking or writing to another, a number of mappings are taking place in their minds, which might go wrong. Fig.2 is an attempt to represent these mappings graphically. 

            Person A                                            Person B

    knowledge --> put into words ----> message ----> interpret --> knowledge

Fig.2: Flow diagram of verbal communication between two human beings}

During his lifetime a human being perceives phenomena (changes or differences), and he associates corresponding concepts - see figure 3 - with them.[3] These concepts make up the knowledge of the human being about the world he is living in.[2]

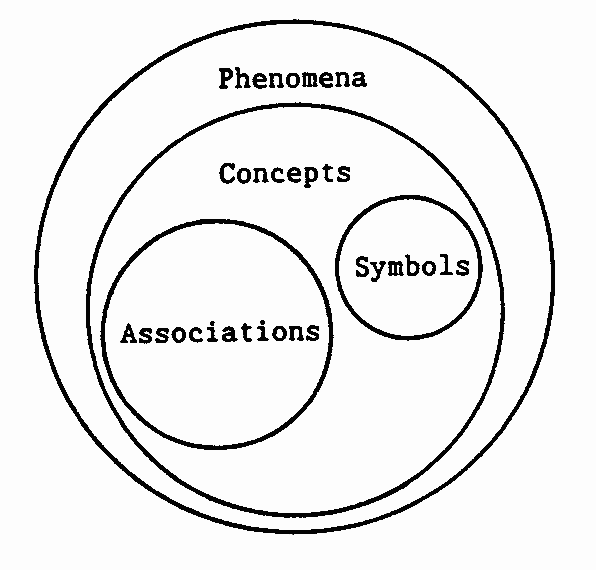
(Image)
Fig.3: The elementary classes.

For example, if the entire universe would have one and the same colour, mankind wouldn't have developed the concept of 'colour'. The perception may be directly (by seeing, hearing etc.) or indirectly (For example by using measuring equipment).

Concepts are also considered to be phenomena.

A symbol is a concept, which by convention is used as a substitute for another concept. This is mostly done for making communication of knowledge possible without directly showing the phenomena about which the knowledge goes. For example, when discussing tables we mostly use the word "table" instead of directly pointing to a table. A completely unambigous communication is possible only when each concept is represented by a unique and distinct symbol. Such a symbol is called the identifier of the concept.

Data is a collection of symbols.

A message is data, being transferred.

If we exclude direct exchange of information by telepathy, and if we exclude the method of directly showing the phenomena about which knowledge has to be communicated - so-called ostensive definition - we can state that human beings communicate knowledge by communicating data - so-called linguistic definition. The way the data is organized is called a language. See the appendix. Only after perceiving the data they associate it with concepts in their mind. In this whole process an improper mapping of knowledge may occur because:

  1. People differ in their way of perception.
  2. People have different knowledge about one and the same subject.
  3. The symbols used may have more than one meaning to the receiver.

Problem 1 is inherent to human nature and we have to live with it. Problems 2 and 3 may be solved when a receiver first learns from the sender what preassumptions he makes. The preassumptions can be seen as a "narrowing" of the semantics of the language they will use.

The semantics of a language consist of definitions: A definition is the association between a linguistic object and the concept it represents. Definitions are represented by specifications. Specification can be done by ostensive definition, or by expressing in more general terms or sentences, up to a level where the probability of misunderstanding is reduced to an acceptable level. The specifications form the ontology of the object world, where the language can be used for making more specific descriptions of the object world.

For natural languages, their ontologies are informal: They are put in narrative form, in general dictionaries. For artificial languages as used for specification of complex objects like electronic products, informal ontologies are not adequate, because they unavoidably contain ambiguities (e.g. homonyms). Also, they cannot be checked by automated means for completeness and absence of contradictions. The development of formal ontologies may solve that problem. A particular form, the IPL ontology, will be discussed below.

Outline of the IPL ontology

The IPL ontology is a kind of a classification scheme, a set of predicates which form a time-independent description of some object world. For a more detailed look we first have to define some additional concepts:

As an example, we will show some formal data about a practical case, and after that we will show the classification scheme which is the base of the formal data.

The tables below are a formal definition of the fact that John Johnson and Evelyn Williams are parents of Mary Johnson.

The table representing the persons: 

   "person" id ;
   ------------------
           "person 1"
           "person 2"
           "person 3"

The tables representing the associations between persons: 

   "person" id       "is father of"  "person" id ;
   ----------------------------------------------------
           "person 2"                        "person 1"


   "person" id       "is mother of"  "person" id ;
   ----------------------------------------------------
           "person 3"                        "person 1"

Elementary states are atomic concepts - they are the "leaves" in networks of associations. The tables representing the elementary states: 

   "first name" proper-name ;
   --------------------------
               "Mary"
               "John"
               "Evelyn"

   "family name" proper-name ;
   ---------------------------
                "Johnson"
                "Williams"

   "sex" adjective;
   ----------------
        "male"
        "female"

The tables representing the associations between elementary states and persons: 

   "first name" proper-name    "is element of"  "person" id ;
   ----------------------------------------------------------------
                "Mary"                                   "person 1"
                "John"                                   "person 2"
                "Evelyn"                                 "person 3"

   "family name" proper-name    "is element of"  "person" id ;
   ----------------------------------------------------------------
                "Johnson"                                "person 1"
                "Johnson"                                "person 2"
                "Williams"                               "person 3"

   "sex" adjective   "is element of"  "person" id ;
   -----------------------------------------------------
        "male"                                "person 2"
        "female"                              "person 1"
        "female"                              "person 3"

id stands for "identification": each phenomenon gets its own unique identification, in order to make later references to any detail possible without changing the existing part of the formal definition.

proper_name and adjective are linguistic terms. Definitions of them can be found in general dictionaries and textbooks of the English Language.

The corresponding classification scheme is obtained by taking an abstract of the formal data. The abstraction is done by copying the heading lines of the tables.

Specification of the classes of elementary states: 

  
        "first name"  proper-name ;
        "family name" proper-name ;
        "sex"         adjective  "male" or "female" ;

Specification of the classes of sets: 

        "person";

Specification of the classes of associations: 

        "first name"   "is element of"  "person";
        "family name"  "is element of"  "person";
        "sex"          "is element of"  "person";


        "person"  "is father of"       "person";
        "person"  "is mother of"       "person";
        "person"  "is grandfather of"  "person";

Rule-classes can be described by logic expressions, with elementary state-, set-, or association class specifications as arguments, for example: 

   "person" z  "is grandfather of"  "person" y

      "is implied by"

       "person" z  "is father of"  "person" x
       and (    "person" x  "is father of"  "person" y
             or "person" x  "is mother of"  "person" y );

x, y and z are identification variables. The rule evaluates to "true" when for a given z and y, a corresponding value of x can be found.

When an ontology also contains rule-classes it is called a knowledge model, and a corresponding data base a knowledge base.

Application of the IPL ontology

Examples:

In these situations communication problems 2 and 3 (as discussed in section 2) have to be avoided at any cost. The only way to do so is by standardizing on a formal ontology which corresponds with the knowledge of the authors. Now arbitrary receivers can learn from the ontology what the data they will receive exactly means. 

  
               <----------- ontology -------------------->
    Person A                                                    Person B
               ----------------> message ----------------> 

Fig.4: Flow diagram of a communication process using a formal ontology

Once the communication problem is solved on the person-to-person level, the problem is implicitly solved on lower levels in the communication path: The only problem left, is the technological problem to get the message physically across, or to get it stored physically.

In general, the IPL ontology is ideal as a base for logic programs, e.g. those written in the Prolog language. In this way there is no distinction between a computer program and its specification, greatly preventing mistakes. The IPL ontology provides the base for more specific theories, which extend it in a tree-like manner.

Detail IPL conventions

The Basics of the notation

The notation is identical to the Prolog one, with additional constraints for the design of ontologies [ISO/IEC 1982] [Lloyd J. 1990, p.177].

Classes and Subclasses

The Prolog syntactical category: 

   <object common noun >( <variable-identifier > ) :-
              <subject common noun > ( <variable-identifier > )

is a specification of the fact that class subject common noun is a subclass of class object common noun. It is a generalization, which means the same as the class of English sentences 

   For all <variable-identifier > holds that
       instance <variable-identifier > 
             of class <subject common noun > 
                     implies instance <variable-identifier > 
                             of class <object common noun >

In other words: 

    An instance of class <subject common noun > 
       is identical to an instance of class <object common noun >

Instance is synonymous to element of the population. In mathematical terms we get
forall i [p(i) => q(i)]
where p stands for <subject common noun> and q stands for <object common noun>. Generalization is one of the two means for defining abstractions. (The other one is aggregation) For example, if we have as Prolog theory 

   human(X) :- male(X). 
   human(X) :- female(X).

(capital letters stand for lexical variables) and as propositions the Prolog facts: 

   male('John').
   male('Harry').
   female('Mary').

we can enter the following queries into the Prolog interpreter, with results as shown below 

  ?-male(X).
      X = 'John'
      X = 'Harry'

  ?-female(X).
      X = 'Mary'

  ?-human(X).
      X = 'John'
      X = 'Harry'
      X = 'Mary'

The last query shows that the Prolog interpreter automatically finds all propositions about instances of subclasses of the class human. We will exploit this feature extensively. In general, a subclass is identified by taking the noun of the superclass, prefixed by another common noun, or an adjective. For example: 

    human(X) :- 
       female_human(X).

A notation with dyadic predicates at the lefthand side and at the righthand side of the implication describes classes and subclasses of associations. For example: 

    human__rents_house(X, Y) :- 
       male_human__rents_house(X, Y).

says that if male X rents house Y then human X rents house Y. For this, the same rules apply as what has been said for monadic predicates.

When the specialization of an association is due to the predicate - and not due to the subject or object - this is normally indicated by prefixing the predicate verb phrase with an additional proverb. For example: 

    human__rents_house(X, Y) :- 
       human__temporarily_rents_house(X, Y).

A positive side-effect of this way of definition is that queries can be performed very efficiently by addressing the proper subclasses. (See the work on many-sorted logics and order-sorted logics by Herbrand 1930, Oberschelp 1962, Schmidt 1938, 1951)

Constraints and inheritance

In the scope of this document, a class is characterized by the constraints imposed on its instances. Constraints are defined in the form [Goebel R. 1986] 

 contradiction(X) :- 
    reference_to_an_inconsistent_set_of_propositions(X).

For example, suppose that all humans in the object world have a passport: 

   human(X) :- male_human(X). 
   human(X) :- female_human(X).

   contradiction(X) :- human(X),
                       not( human__has_passport(X,_) ).

(The comma stands for 'logical and'.) A check on inconsistencies in the specification is initiated by querying for contradiction(H). The Prolog interpreter will report all values of H for which inconsistencies are detected. In the example, a contradiction is reported when a proposition of the form male_human(X) or female_human(X) is found for which no proposition of the form human__has_passport(H, P) has been defined. In the theories, ~(X) stands for not(X).

The example shows how a constraint is defined in terms of the class name | human here | while the query for contradictions automatically checks the subclasses male_human and female_human for this particular constraint. This inheritance of constraints is fundamental: An instance of a class inherits the constraints imposed on instances of the corresponding superclasses.

Note that this type of inheritance is fundamentally different from the type of inheritance used in Object Oriented Programming. It is however identical to the mechanism underlying strict subtyping of data in programming languages. Now we can also define the formal reason for having subclasses: A subclass should have at least one constraint which is disjoint from the constraints of its superclass(es) as well as from the constraints of its sibling class(es). Whether the populations of two sibling classes intersect each other|or not|depends on the constraints imposed on them.

For associations which are the closing clause in a transitive closure, the verb phrase equals the verb phrase of the closure defining clause, prefixed with is_explicitly_. For example: 

    set__is_subset_of_set(X, Y) :- 
       set__is_explicitly_subset_of_set(X, Y).

    set__is_subset_of_set(X, Y) :- 
       set__is_explicitly_subset_of_set(X, Z).
       set__is_subset_of_set(Z, Y).

Appendix: A refresher on linguistic analysis

A simplified view will be given, sufficient for reading this document. In linguistic analysis the following levels of abstraction are distinguished:

As an example we will analyze the sentence:

"The dog bites the girl"

The analysis is given in the order as applied in practice. 

   1. Technological Analysis:

      - Font: Times Roman

      - Material: Black ink on white paper

   The sentence is readable, so it is technologically correct.

   2. Syntactical Analysis:

   The words in the sentence are of the English language:

      - "the" is a determiner
      - "dog" is a common noun
      - "bites" is a verb
      - "the" is a determiner
      - "girl" is a common noun

   The sequence:

             determiner noun verb determiner noun

   conforms to the syntax of the English language, so it is
   syntactically correct. It is a declarative sentence.

   3. Semantical Analysis:

   A declarative sentence in the English language has the form:

             subject-phrase predicate object-phrase

      - Subject-phrase: "the dog"
      - Predicate: "bites"
      - Object-phrase: "the girl"

   The sentence describes a situation which could have been perceived in the
   real world, so it is semantically correct.

For a comparison of semantical with syntactical analysis we will analyze the sentence:

"the wall bites the dog"

Although this sentence conforms to the syntax of the English language, the ontology that most people assume about dogs and walls says that it is absolutely impossible that that walls bite dogs. So they will conclude that for "the wall" as subject phrase, "bites" cannot be a predicate, nor "the dog" be an object phrase. This implies that this sentence is semantically incorrect, in other terms, that it is false. This will change only as soon as people really have seen a wall biting a dog.

In the context of this document the term "language" has to be taken in a very general sense: the analysis presented above applies not only to written text but also to spoken text, electronic messages, schematic diagrams, data in data bases etc.